As one of the most popular programming languages out there, many people want to learn Python. But how do you go about getting started? In this guide, we explore everything you need to know to begin your learning journey, including a step-by-step guide and learning plan and some of the most useful resources to help you succeed.
What is Python?
Python is a high-level, interpreted programming language created by Guido van Rossum and first released in 1991. It is designed with an emphasis on code readability, and its syntax allows programmers to express concepts in fewer lines of code than would be possible in languages such as C++ or Java.
Python supports multiple programming paradigms, including procedural, object-oriented, and functional programming. In simpler terms, this means it’s flexible and allows you to write code in different ways, whether that's like giving the computer a to-do list (procedural), creating digital models of things or concepts (object-oriented), or treating your code like a math problem (functional).
What makes Python so popular?
As of January 2024, Python remains the most popular programing language according to the TIOBE index. Over the years, Python has become one of the most popular programming languages due to its simplicity, versatility, and wide range of applications.
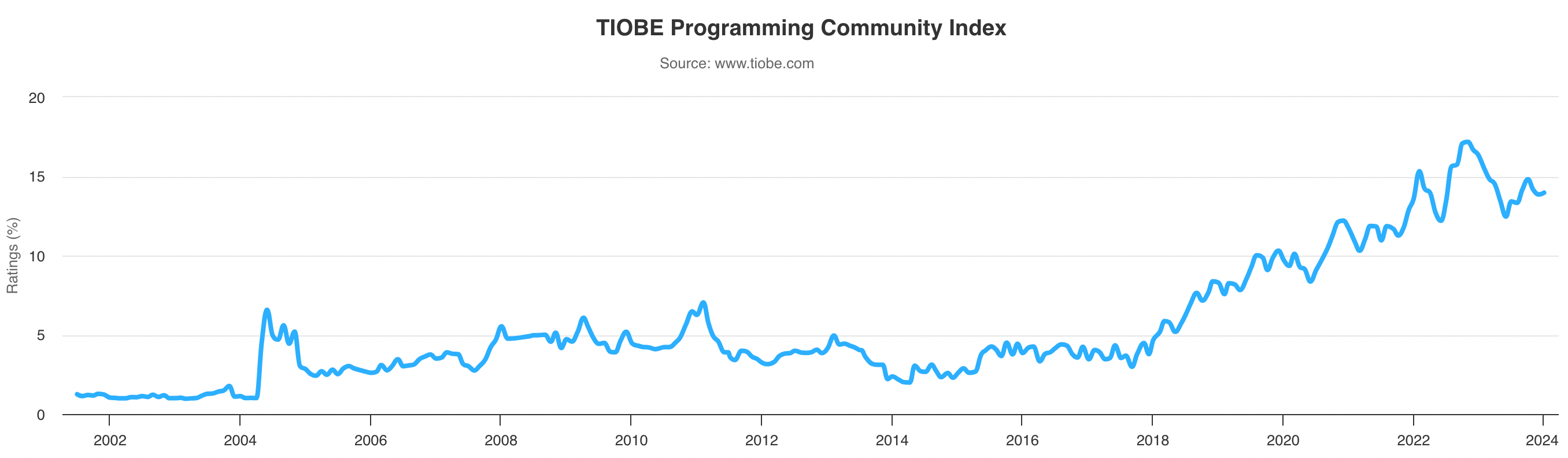
The popularity of Python
These reasons also mean it is a highly favored language for data science as it allows data scientists to focus more on data interpretation rather than language complexities.
Let’s explore these factors in more detail.
The main features of Python
Let’s have a close look at some of the Python features that make it such a versatile and widely-used programming language:
- Readability. Python is known for its clear and readable syntax, which resembles English to a certain extent.
- Easy to learn. Python’s readability makes it relatively easy for beginners to pick up the language and understand what the code is doing.
- Versatility. Python is not limited to one type of task; you can use it in many fields. Whether you're interested in web development, automating tasks, or diving into data science, Python has the tools to help you get there.
- Rich library support. It comes with a large standard library that includes pre-written code for various tasks, saving you time and effort. Additionally, Python's vibrant community has developed thousands of third-party packages, which extend Python's functionality even further.
- Platform independence. One of the great things about the language is that you can write your code once and run it on any operating system. This feature makes Python a great choice if you're working on a team with different operating systems.
- Interpreted language. Python is an interpreted language, which means the code is executed line by line. This can make debugging easier because you can test small pieces of code without having to compile the whole program.
- Open source and free. It’s also an open-source language, which means its source code is freely available and can be distributed and modified. This has led to a large community of developers contributing to its development and creating a vast ecosystem of Python libraries.
- Dynamically typed. Python is dynamically typed, meaning you don't have to declare the data type of a variable when you create it. The Python interpreter infers the type, which makes the code more flexible and easy to work with.
Why is learning Python so beneficial?
Learning Python is beneficial for a variety of reasons. Besides its wide popularity, Python has applications in numerous industries, from tech to finance, healthcare, and beyond. Learning Python opens up many career opportunities and guarantees improved career outcomes. Here's how:
Python has a variety of applications
We’ve already mentioned the versatility of Python, but let’s look at a few specific examples of where you can use it:
- Data science. Python is widely used in data analysis and visualization, with libraries like Pandas, NumPy, and Matplotlib being particularly useful.
- Web development. Frameworks such as Django and Flask are used for backend web development.
- Software development. You can use Python in software development for scripting, automation, and testing.
- Game development. You can even use it for game development using libraries like PyGame and tkinter.
- Machine learning & AI. Libraries like TensorFlow, PyTorch, and Scikit-learn make Python a popular choice in this field. Find out how to learn AI in a separate guide.
There is a demand for Python skills
With the rise of data science, machine learning, and artificial intelligence, there is a high demand for Python skills. According to a 2022 report from GitHub, Python usage increased 22.5% year on year, making it the third-most used language on the platform.
Companies across many industries are looking for professionals who can use Python to extract insights from data, build machine learning models, and automate tasks. Python certifications are also in demand.
Learning Python can significantly enhance your employability and open up a wide range of career opportunities. A quick search on the recruitment website Indeed for ‘Python’ finds over 60,000 jobs in the US requiring the skill.
How Long Does it Take to Learn Python?
While Python is one of the easier programming languages to learn, it still requires dedication and practice. The time it takes to learn Python can vary greatly depending on your prior experience with programming, the complexity of the concepts you're trying to grasp, and the amount of time you can dedicate to learning.
However, with a structured learning plan and consistent effort, you can often grasp the basics in a few weeks and become somewhat proficient in a few months.
Online resources can give you a firm basis for your skills and can range in length. As an example, our Python Programming skill track, covering the skills needed to code proficiently, takes around 24 study hours to complete, while our Data Analyst with Python career track takes around 36 study hours. Of course, the journey to becoming a true Pythonista is a long-term process, and much of your efforts will need to be self-study alongside more structured methods.
As a comparison of how long it takes to learn Python vs other languages:
|
Language |
Time to Learn |
|
Python |
1-3 months for basics, 4-12 months for advanced topics |
|
SQL |
1 to 2 months for basics, 1-3 months for advanced topics |
|
R |
1-3 months for basics, 4-12 months for advanced topics |
|
Julia |
1-3 months for basics, 4-12 months for advanced topics |
|
* The above comparisons are purely based on timelines needed to learn to become proficient with a programming language, not timelines needed to break into a career. Moreover, each person learns differently and goes at their own pace, we only aim to provide a framework with these timelines. |
|
A comparison table of how long it would take to learn different programming languages
How to Learn Python: 6 Steps for Success
Let’s take a look at how you can go about learning Python. This step-by-step guide assumes you’re at learning Python from scratch, meaning you’ll have to start with the very basics and work your way up.
1. Understand why you’re learning Python
Firstly, it’s important to figure out your motivations for wanting to learn Python. It’s a versatile language with all kinds of applications. So, understanding why you want to learn Python will help you develop a tailored learning plan.
Whether you're interested in automating tasks, analyzing data, or developing software, having a clear goal in mind will keep you motivated and focused on your learning journey. Some questions to ask yourself might include:
- What are my career goals? Are you aiming for a career in data science, web development, software engineering, or another field where Python is commonly used?
- What problems am I trying to solve? Are you looking to automate tasks, analyze data, build a website, or create a machine learning model? Python can be used for all these tasks and more.
- What interests me? Are you interested in working with data or building applications? Or perhaps you're intrigued by artificial intelligence? Your interests can guide your learning journey.
- What is my current skill level? If you're a beginner, Python's simplicity and readability make it a great first language. If you're an experienced programmer, you might be interested in Python because of its powerful libraries and frameworks.
The answers to these questions will determine how to structure your learning path, which is especially important for the following steps.
Python is one of the easiest programming languages to pick up. What's really nice is that learning Python doesn't pigeonhole you into one domain; Python is so versatile it has applications in software development, data science, artificial intelligence, and almost any role that has programming involved with it!
Richie Cotton, Data Evangelist at DataCamp
2. Get started with the Python basics
Understanding Python Basics
Python emphasizes code readability and allows you to express concepts in fewer lines of code. You’ll want to start by understanding basic concepts such as variables, data types, and operators.
Our Introduction to Python course covers the basics of Python for data analysis, helping you get familiar with these concepts.
Installing Python and setting up your environment
To start coding in Python, you need to install Python and set up your development environment. You can download Python from the official website, use Anaconda Python, or start with DataCamp Workspace to get started with Python in your browser.
DataCamp Workspace
Skip the installation process, and get started with Python on your browser using DataCamp Workspace
Full a full explanation of getting set up, check out our guide to how to install Python.
Write your first Python program
Start by writing a simple Python program, such as a classic "Hello, World!" script. This process will help you understand the syntax and structure of Python code. Our Python tutorial for beginners will take you through some of these basics.
Python data structures
Python offers several built-in data structures like lists, tuples, sets, and dictionaries. These data structures are used to store and manipulate data in your programs. We have a course dedicated to data structures and algorithms in Python, which covers a wide range of these aspects.
Control flow in Python
Control flow statements, like if-statements, for-loops, and while-loops, allow your program to make decisions and repeat actions. We have a tutorial on if statements, as well as ones on while-loops and for-loops.
Functions in Python
Functions in Python are blocks of reusable code that perform a specific task. You can define your own functions and use built-in Python functions. We have a course on writing functions in Python which covers the best practices for writing maintainable, reusable, complex functions.
3. Master intermediate Python concepts
Once you’re familiar with the basics, you can start moving on to some more advanced topics. Again, these are essential for building your understanding of Python and will help you tackle an array of problems and situations you may encounter when using the programming language.
Error handling and exceptions
Python provides tools for handling errors and exceptions in your code. Understanding how to use try/except blocks and raise exceptions is crucial for writing robust Python programs. We’ve got a dedicated guide on exception and error handling in Python which can help you troubleshoot your code.
Working with libraries in Python
Python's power comes from its vast ecosystem of libraries. Learn how to import and use common libraries like NumPy for numerical computing, pandas for data manipulation, and matplotlib for data visualization. In a separate article, we cover the top Python libraries for data science, which can provide more context for these tools.
Object-oriented programming in Python
Python supports object-oriented programming (OOP), a paradigm that allows you to structure your code around objects and classes. Understanding OOP concepts like classes, objects, inheritance, and polymorphism can help you write more organized and efficient code.
To learn more about object-oriented programming in Python, check out our online course, which covers how to create classes and leverage techniques such as inheritance and polymorphism to reuse and optimize your code.
4. Learn by doing
One of the most effective ways to learn Python is by actively using it. You want to minimize the amount of time you spend on learning syntax and work on projects as soon as possible. This learn-by-doing approach involves applying the concepts you've learned through your studies to real-world projects and exercises.
Thankfully, many DataCamp resources use this learn-by-doing method, but here are some other ways to practice your skills:
- Take on projects that challenge you. Work on projects that interest you. This could be anything from a simple script to automate a task, a data analysis project, or even a web application.
- Attend webinars and code-alongs. You’ll find plenty of DataCamp webinars and online events where you can code along with the instructor. This method can be a great way to learn new concepts and see how they're applied in real-time.
- Apply what you've learned to your own ideas and projects. Try to recreate existing projects or tools that you find useful. This can be a great learning experience as it forces you to figure out how something works and how you can implement it yourself.
A range of Python projects on DataCamp Projects
5. Build a portfolio of projects
As you complete projects, compile them into a portfolio. This portfolio should reflect your skills and interests and be tailored to the career or industry you're interested in. Try to make your projects original and showcase your problem-solving skills.
We’ve got a list of 60+ Python projects for all levels in a separate article, but here are a few suggested project ideas for different levels:
- Beginners. Simple projects like a number guessing game, a to-do list application, or a basic data analysis using a dataset of your interest.
- Intermediate. More complex projects like a web scraper, a blog website using Django, or a machine learning model using Scikit-learn.
- Advanced. Large-scale projects like a full-stack web application, a complex data analysis project, or a deep learning model using TensorFlow or PyTorch.
We’ve got a full guide on how to build a great data science portfolio, which covers a variety of different examples. And don’t forget; you can build your portfolio with DataCamp to show off your skills.
6. Keep challenging yourself
Never stop learning. Once you've mastered the basics, look for more challenging tasks and projects. Specialize in areas that are relevant to your career goals or personal interests. Whether it's data science, web development, or machine learning, there's always more to learn in the world of Python. Remember, the journey of learning Python is a marathon, not a sprint. Keep practicing, stay curious, and don't be afraid to make mistakes.
An Example Python Learning Plan
Below, we’ve created a potential learning plan outlining where to focus your time and efforts if you’re just starting out with Python. Remember, the timescales, subject areas, and progress all depend on a wide range of variables. We want to make this plan as hands-on and practical as possible, which is why we’ve recommended projects you can work on as you progress.
Month 1-3: Basics of Python and data manipulation
Master basic and intermediate programming concepts. Start doing basic projects in your specialized field. For example, if you're interested in data science, you might start by analyzing a dataset using pandas and visualizing the data with matplotlib.
- Python basics. Start with the fundamentals of Python. This includes understanding the syntax, data types, control structures, functions, and more.
- Data manipulation. Learn how to handle and manipulate data using Python libraries like pandas and NumPy. This is a crucial skill for any Python-related job, especially in data science and machine learning.
Recommended resources & projects
- Python Fundamentals
- Investigating Netflix Movies and Guest Stars in The Office Data Science Project
- Python Cheat Sheet for Beginners
Month 4-6: Intermediate Python
Now that you have a solid foundation, you can start learning more advanced topics.
- Intermediate Python. Once you're comfortable with the basics, move on to more advanced Python topics. This includes understanding object-oriented programming, error handling, and more complex data structures. Explore more advanced topics like decorators, context managers, metaclasses, and more.
- More specific topics. If you're interested in machine learning, for example, you might start the Machine Learning Fundamentals with Python Track. Continue to work on projects, but make them more complex. For example, you might build a machine learning model to predict house prices or classify images.
Recommended resources & projects
- Python Programmer Career Track
- A New Era of Data Analysis in Baseball Project
- Object-Oriented Programming in Python (OOP): Tutorial
Month 7 onwards: Advanced Python and specialization
At this point, you should have a good understanding of Python and its applications in your field of interest. Now is the time to specialize.
- Specialization. Based on your interests and career aspirations, specialize in one area. This could be data science, machine learning, web development, automation, or any other field. For instance, If you're interested in natural language processing, you might start learning about libraries like NLTK and SpaCy. Keep working on projects and reading about new developments in your field.
Recommended resources & projects
- Machine Learning Scientist with Python Career Track
- Naïve Bees: Image Loading and Processing Project
- Mastering Natural Language Processing (NLP) with PyTorch: Comprehensive Guide
6 Top Tips for Learning Python
If you’re eager to start your Python learning journey, it’s worth bearing these tips in mind; they’ll help you maximize your progress and keep focused.
1. Choose Your Focus
Python is a versatile language with a wide range of applications, from web development and data analysis to machine learning and artificial intelligence. As you start your Python journey, it can be beneficial to choose a specific area to focus on. This could be based on your career goals, personal interests, or simply the area you find most exciting.
Choosing a focus can help guide your learning and make it more manageable. For example, if you're interested in data science, you might prioritize learning libraries like pandas and NumPy. If web development is your goal, you might focus on frameworks like Django or Flask.
Remember, choosing a focus doesn't mean you're limited to that area. Python's versatility means that skills you learn in one area can often be applied in others. As you grow more comfortable with Python, you can start exploring other areas and expanding your skill set.
2. Practice regularly
Consistency is a key factor in successfully learning a new language, and Python is no exception. Aim to code every day, even if it's just for a few minutes. This regular practice will help reinforce what you've learned, making it easier to recall and apply.
Daily practice doesn't necessarily mean working on complex projects or learning new concepts each day. It could be as simple as reviewing what you've learned, refactoring some of your previous code, or solving coding challenges.
3. Work on real projects
The best way to learn Python is by using it. Working on real projects gives you the opportunity to apply the concepts you've learned and gain hands-on experience. Start with simple projects that reinforce the basics, and gradually take on more complex ones as your skills improve. This could be anything from automating a simple task, building a small game, or even creating a data analysis project.
4. Join a community
Learning Python, like any new skill, doesn't have to be a solitary journey. In fact, joining a community of learners can provide a wealth of benefits. It can offer support when you're facing challenges, provide motivation to keep going, and present opportunities to learn from others.
There are many Python communities you can join. These include local Python meetups, where you can connect with other Python enthusiasts in person and online forums where you can ask questions, share your knowledge, and learn from others' experiences.
5. Don't rush
Learning to code takes time, and Python is no exception. Don't rush through the material in an attempt to learn everything quickly. Take the time to understand each concept before moving on to the next. Remember, it's more important to fully understand a concept than to move through the material quickly.
6. Keep iterating
Learning Python is an iterative process. As you gain more experience, revisit old projects or exercises and try to improve them or do them in a different way. This could mean optimizing your code, implementing a new feature, or even just making your code more readable. This process of iteration will help reinforce what you've learned and show you how much you've improved over time.
The Best Ways to Learn Python in 2024
There are many ways that you can learn Python, and the best way for you will depend on how you like to learn and how flexible your learning schedule is. Here are some of the best ways you can start learning Python from scratch today:
Online courses
Online courses are a great way to learn Python at your own pace. We offer over 150 Python courses for all levels, from beginners to advanced learners. These courses often include video lectures, quizzes, and hands-on projects, providing a well-rounded learning experience.
If you’re totally new to Python, you might want to start with our Introduction to Python course. For those looking to grasp all the essentials, our Python Fundamentals skill track covers everything you need to start programming.
Top Python courses for beginners
- Python Fundamentals Skill Track
- Python Programmer Career Track
- Introduction to Python
- Python Data Science Toolbox
- Writing Efficient Python Code
Tutorials
Tutorials are a great way to learn Python, especially for beginners. They provide step-by-step instructions on how to perform specific tasks or understand certain concepts in Python.
We have a wide range of tutorials available related to Python and associated libraries. So whether you’re just getting started or hoping to improve your existing knowledge, you’re sure to find topics of interest.
Top Python tutorials
- Python Tutorial for Beginners
- How to install Python
- 30 Cool Tricks for Better Python Code
- 21 Essential Python Tools
Cheat sheets
If you’re looking for a fast way to brush up on specific Python principles, cheat sheets are a handy way to have a lot of knowledge in one resource. For example, our Python Cheat Sheet for Beginners covers many of the core concepts you’ll need to get started.
We also have cheat sheets for specific Python libraries, such as Seaborn and SciPy, which include example code snippets and tips to get the most out of the tools.

A selection of cheat sheets
Top Python cheat sheets
- Python Cheat Sheet for Beginners
- Working with Dates and Times in Python Cheat Sheet
- Python Data Visualization: Bokeh Cheat Sheet
- Importing Data in Python Cheat Sheet
Projects
Working on projects helps you utilize the skills you’ve learned already to tackle new challenges. As you work your way through, you’ll need to adapt your approach and research new ways of getting results, helping you to master new Python techniques.
You can find a whole range of data science projects to work on at DataCamp. These allow you to apply your coding skills to a wide range of datasets to solve real-world problems in your browser, and you can filter specifically by those that require Python.
Top Python projects
- 60+ Python Projects for All Levels of Expertise
- Exploring the History of Lego
- Investigating Netflix Movies and Guest Stars in The Office
- NYC Airbnb Data Analysis
Books
Books are an excellent resource for learning Python, especially for those who prefer self-paced learning. Learn Python the Hard Way by Zed Shaw and Python Crash Course by Eric Matthes are two highly recommended books for beginners. These books provide in-depth explanations of Python concepts along with numerous exercises and projects to reinforce your learning.
Top Python books
- Learning Python, 5th Edition: Lutz, Mark
- Head First Python: A Brain-Friendly Guide: Barry, Paul
- Python Distilled (Developer's Library): Beazley, David
- Python 3: The Comprehensive Guide to Hands-On Python Programming
The Top Python Careers in 2024
As we’ve already seen, demand for professionals with Python skills is increasing, and there are many roles out there that require knowledge of the programming language. Here are some of the top careers that use Python you can choose from:
Data scientist
Data scientists are the detectives of the data world, responsible for unearthing and interpreting rich data sources, managing large amounts of data, and merging data points to identify trends.
They utilize their analytical, statistical, and programming skills to collect, analyze, and interpret large datasets. They then use this information to develop data-driven solutions to challenging business problems.
Part of these solutions is developing machine learning algorithms that generate new insights (e.g., identifying customer segments), automate business processes (e.g., credit score prediction), or provide customers with newfound value (e.g., recommender systems).
Key skills:
- Strong knowledge of Python, R, and SQL
- Understanding of machine learning and AI concepts
- Proficiency in statistical analysis, quantitative analytics, and predictive modeling
- Data visualization and reporting techniques
- Effective communication and presentation skills
Essential tools:
- Data analysis tools (e.g., pandas, NumPy)
- Machine learning libraries (e.g., Scikit-learn)
- Data visualization tools (e.g., Matplotlib, Tableau)
- Big data frameworks (e.g., Airflow, Spark)
- Command line tools (e.g., Git, Bash)
Python developer
Python developers are responsible for writing server-side web application logic. They develop back-end components, connect the application with the other web services, and support the front-end developers by integrating their work with the Python application. Python developers are also often involved in data analysis and machine learning, leveraging the rich ecosystem of Python libraries.
Key skills:
- Proficiency in Python programming
- Understanding of front-end technologies (HTML, CSS, JavaScript)
- Knowledge of Python web frameworks (e.g., Django, Flask)
- Familiarity with ORM libraries
- Basic understanding of database technologies (e.g., MySQL, PostgreSQL)
Essential tools:
- Python IDEs (e.g., PyCharm)
- Version control systems (e.g., Git)
- Python libraries for web development (e.g., Django, Flask)
Data analyst
Data analysts are responsible for interpreting data and turning it into information that can offer ways to improve a business. They gather information from various sources and interpret patterns and trends. Once data has been gathered and interpreted, Data analysts can then report back what they've found to the wider business to influence strategic decisions.
Key skills:
- Proficiency in Python, R, and SQL
- Strong knowledge of statistical analysis
- Experience with business intelligence tools (e.g., Tableau, Power BI)
- Understanding of data collection and data cleaning techniques
- Effective communication and presentation skills
Essential tools:
- Data analysis tools (e.g., pandas, NumPy)
- Business intelligence data tools (e.g., Tableau, Power BI)
- SQL databases (e.g., MySQL, PostgreSQL)
- Spreadsheet software (e.g., MS Excel)
Machine learning engineer
Machine learning engineers are sophisticated programmers who develop machines and systems that can learn and apply knowledge. These professionals are responsible for creating programs and algorithms that enable machines to take action without being specifically directed to perform those tasks.
Key skills:
- Proficiency in Python, R, and SQL
- Deep understanding of machine learning algorithms
- Knowledge of deep learning frameworks (e.g., TensorFlow,)
Essential tools:
- Machine learning libraries (e.g., Scikit-learn, TensorFlow, PyTorch)
- Data analysis and manipulation tools (e.g., pandas, NumPy)
- Data visualization tools (e.g., Matplotlib, Seaborn)
- Deep learning frameworks (e.g., TensorFlow, Keras, PyTorch)
|
Role |
Description |
Key Skills |
Tools |
|
Data Scientist |
Extracts insights from data to solve business problems and develop machine learning algorithms. |
Python, R, SQL, Machine Learning, AI concepts, statistical analysis, data visualization, communication |
Pandas, NumPy, Scikit-learn, Matplotlib, Tableau, Airflow, Spark, Git, Bash |
|
Python Developer |
Writes server-side web application logic, develops back-end components, and integrates front-end work with Python applications. |
Python programming, front-end technologies (HTML, CSS, JavaScript), Python web frameworks (Django, Flask), ORM libraries, database technologies |
PyCharm, Jupyter Notebook, Git, Django, Flask, Pandas, NumPy |
|
Data Analyst |
Interprets data to offer ways to improve a business, and reports findings to influence strategic decisions. |
Python, R, SQL, statistical analysis, data visualization, data collection and cleaning, communication |
Pandas, NumPy, Matplotlib, Tableau, MySQL, PostgreSQL, MS Excel |
|
Machine Learning Engineer |
Develops machines and systems that can learn and apply knowledge, and creates programs and algorithms for machine learning. |
Python, R, SQL, machine learning algorithms, deep learning frameworks |
Scikit-learn, TensorFlow, PyTorch, Pandas, NumPy, Matplotlib, Seaborn, TensorFlow, Keras, PyTorch |
A comparison table of jobs that use Python
How to Find a Job That Uses Python
A degree can be a great asset when starting a career that uses Python, but it's not the only pathway. While a formal education in computer science or a related field can be beneficial, more and more professionals are entering the field through non-traditional routes. With dedication, consistent learning, and a proactive approach, you can land your dream job that uses Python.
Here's how to find a job that uses Python without a degree:
Keep learning about the field
Stay updated with the latest developments in Python. Follow influential Python professionals on Twitter, read Python-related blogs, and listen to Python-related podcasts. Some of the Python thought leaders to follow include Guido van Rossum (the creator of Python), Raymond Hettinger, and others. You'll gain insights into trending topics, emerging technologies, and the future direction of Python.
You should also check out industry events, whether it’s webinars at DataCamp, Python conferences, or networking events.
Develop a portfolio
Building a strong portfolio that demonstrates your skills and completed projects is one way to differentiate yourself from other candidates. Importantly, showcasing projects where you've applied Python to address real-world challenges can leave a lasting impression on hiring managers.
As Nick Singh, author of Ace the Data Science Interview, said on the DataFramed Careers Series podcast,
The key to standing out is to show your project made an impact and show that other people cared. Why are we in data? We're trying to find insights that actually impact a business, or we're trying to find insights that will actually shape society or create something novel. We're trying to improve profitability or improve people's lives using and analyzing data, so if you don’t somehow quantify the impact, then you are lacking impact.
Nick Singh, Author of Ace the Data Science Interview
Your portfolio should be a diverse showcase of projects that reflect your Python expertise and its various applications. For further guidance on crafting an impressive data science portfolio, refer to our dedicated article on the topic.
Develop an effective resume
In the modern job market, your resume needs to impress not just human recruiters but also Applicant Tracking Systems (ATS). These automated software systems are used by many companies to sift through resumes and eliminate those that don't meet specific criteria. As a result, it's essential to optimize your resume to be both ATS-friendly and compelling to hiring managers.
According to Jen Bricker, former Head of Career Services at DataCamp:
60% to 70% of applications get shifted out of consideration before humans actually look at the application.
Jen Bricker, Former Head of Career Services at DataCamp
Therefore, it's crucial to structure your resume as effectively as possible. For more insights on creating a standout data scientist resume, check out our separate article on the subject.
Get noticed by hiring managers
Proactive engagement on social platforms can help you catch the attention of hiring managers. Share your projects and thoughts on platforms like LinkedIn or Twitter, participate in Python communities, and contribute to open-source projects. These activities not only increase your visibility but also demonstrate your enthusiasm for Python.
Remember, forging a career in a field that utilizes Python requires persistence, ongoing learning, and patience. But by following these steps, you're well on your way to success.
Final Thoughts
Learning Python is a rewarding journey that can open up a multitude of career opportunities. This guide has provided you with a roadmap to start your Python learning journey, from understanding the basics to mastering advanced concepts and working on real-world projects.
Remember, the key to learning Python (or any programming language) is consistency and practice. Don't rush through the concepts. Take your time to understand each one and apply it in practical projects. Join Python communities, participate in coding challenges, and never stop learning.
FAQs
What is Python?
Python is a high-level, interpreted programming language known for its clear and readable syntax. It supports multiple programming paradigms, including procedural, object-oriented, and functional programming, making it a versatile and flexible language.
What are the main features of Python?
Python is known for its readability and ease of learning. It is versatile, with applications in many fields, and has rich library support. Python is platform-independent, meaning it can run on any operating system. It's an interpreted language, which aids in debugging, and it's open-source and free. Python is also dynamically typed, enhancing code flexibility.
What are some applications of Python?
Python is widely used in data analysis and visualization, backend web development, software development for scripting, automation, and testing, game development, and machine learning & AI.
How long does it take to learn Python?
The time it takes to learn Python can vary greatly, but with a structured learning plan and consistent effort, you can often grasp the basics in a few weeks and become somewhat proficient in a few months. The journey to becoming a true Pythonista is a long-term process, requiring both structured learning and self-study.
Is Python difficult to learn?
Python is often considered one of the easier programming languages to learn for beginners due to its clear and readable syntax, which resembles English to a certain extent. Its design emphasizes code readability, and its syntax allows programmers to express concepts in fewer lines of code than many other languages. However, like any language, mastering Python requires dedication and practice. With a structured learning plan and consistent effort, beginners can often grasp the basics in a few weeks and become somewhat proficient in a few months.
What are some job roles that use Python?
Roles that use Python include Data Scientist, Python Developer, Data Analyst, and Machine Learning Engineer. Each of these roles may require proficiency in Python and other specific skills and tools.
Do I need to be good at math to learn Python?
Basic math skills are sufficient for starting with Python. As you delve into specific fields like data science or machine learning, more advanced math might be needed.
What is the difference between Python 2 and Python 3?
Python 2 and Python 3 are different versions of the Python language. Python 3, the latest version, has several improvements and changes that make it more efficient and powerful. Python 2 is no longer maintained.

A writer and content editor in the edtech space. Committed to exploring data trends and enthusiastic about learning data science.

Adel is a Data Science educator, speaker, and Evangelist at DataCamp where he has released various courses and live training on data analysis, machine learning, and data engineering. He is passionate about spreading data skills and data literacy throughout organizations and the intersection of technology and society. He has an MSc in Data Science and Business Analytics. In his free time, you can find him hanging out with his cat Louis.
Exploring Matplotlib Inline: A Quick Tutorial
How to Use the NumPy linspace() Function
Python Absolute Value: A Quick Tutorial
How to Check if a File Exists in Python
Writing Custom Context Managers in Python
Bex Tuychiev